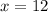Answer:
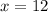
Explanation:
Given
Shapes: Square and Rectangle
Square:
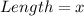
Rectangle:
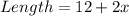
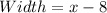
Required
Find x
First, we calculate the area of the square.
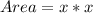
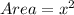
Next, we calculate the area of the rectangle
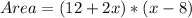
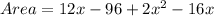
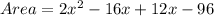
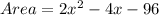
Since both areas are equal, we have:

Equate to 0
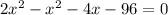
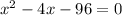
Expand:
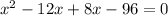
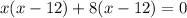
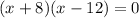
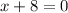 or
or
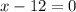
 or
or
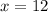
But x can't be negative.
Hence: