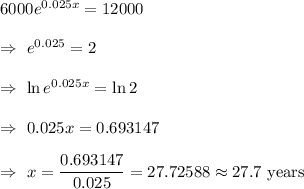Question

$6,000 is invested in an account at interest rate r, compounded continuously. Find the time (in years) required for the amount to double when r= 9.5% and when r=2.5%.

Answer 1

Answer: When r= 9.5% , time = 7.3 years

When r= 2.5% , time = 27.7 years

Explanation:

Exponential equation for compounded continuously:

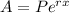`A=Pe^(rx)` , where P= Principal value invested , r= rate of interest, x= time

Given : P= $6,000

A = 2P= 2 ($6,000) = $12,000 (i)

When r= 9.5%= 0.095

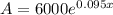`A= 6000e^(0.095x)` (ii)

From (i) and (ii)

`6000e^(0.095x)=12000\\\\\Rightarrow\ e^(0.095x)=2\\\\\Rightarrow\ \ln e^(0.095x) =\ln 2\\\\\Rightarrow\ 0.095x=0.693147\\\\\Rightarrow\ x=(0.693147)/(0.095)=7.296284210\approx7.3 \text{ years}`

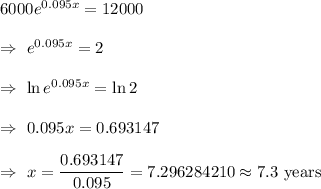
For r= 2.5% = 0.025

`6000e^(0.025x)=12000\\\\\Rightarrow\ e^(0.025)=2\\\\\Rightarrow\ \ln e^(0.025x) =\ln 2\\\\\Rightarrow\ 0.025x=0.693147\\\\\Rightarrow\ x=(0.693147)/(0.025)=27.72588\approx27.7 \text{ years}`