Answer:
(a) -6.67
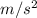
(b) 0.68
Step-by-step explanation:
Given that the mass of the truck,
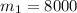 kg.
kg.
Mass of the package,
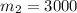 kg.
kg.
As the package does not slide, so the acceleration of both, truck as well as the package, is the same.
Let
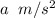 is the acceleration of the combined mass, m.
is the acceleration of the combined mass, m.
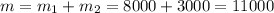 kg.
kg.
The initial velocity of the combined mass, u= 20 m/s.
Time required to stop, t=3 seconds.
Final velocity, v=0.
Displacement traveled, s=50 m.
(a) As
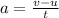
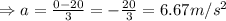
Hence the acceleration of the truck is
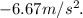
(b) Now,
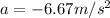 is the acceleration of the package, this acceleration is due the frictional force, f.
is the acceleration of the package, this acceleration is due the frictional force, f.
Due to inertia, on application of break, the package have tendency to slide to left (in the direction of velocity). But the package does not slides, this is only due to the frictional force, f, which acts in the right direction ( opposite to the direction of velocity).
So, the magnitude of frictional force required on
 to avoid slide is
to avoid slide is
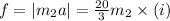
Now, let \mu be the minimum coefficient of the friction, so
The force due to friction,
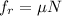 ,
,
where
 is the normal reaction.
is the normal reaction.
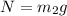 , where g is the acceleration due to gravity.
, where g is the acceleration due to gravity.
So,
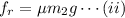
To avoid slide,
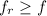
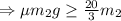 [from (i)and (ii)]
[from (i)and (ii)]
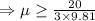
![[ as \;g=9.81 m/s^2]](https://img.qammunity.org/2021/formulas/physics/high-school/629h50xg2ccyzu4pb8pbm9nglyj79lo4hn.png)
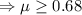
Hence, the minimum value of coefficient of friction between packages and the truck os 0.68.