Question

12) which of the following is factor of the polynomial x^4+x^3-x^2+x-1

x+1
x-1
Both options 1 and 2
None​

Answer 1

Answer: None

Explanation:

Polynomial Remainder Theorem

The polynomial remainder theorem establishes that the remainder of the division of a polynomial f(x) by (x-k) is equal to f(k), that is, substituting x for k.

We are given the polynomial:

`f(x)= x^4+x^3-x^2+x-1`

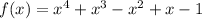
And it's required to know if (x+1) and/or (x-1) are factors of the polynomial.

We apply the theorem for both cases.

For (x+1), we substitute x=-1 into the polynomial:

`f(-1)= (-1)^4+(-1)^3-(-1)^2+(-1)-1`

`f(-1)= 1-1-1-1-1=-3`

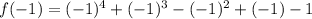
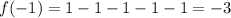
Since the remainder is not zero, x+1 is not a factor of the given polynomial.

For (x-1), we substitute x=1 into the polynomial:

`f(-1)= (1)^4+(1)^3-(1)^2+(1)-1`

`f(-1)= 1+1-1+1-1=1`

Since the remainder is not zero, x-1 is not a factor of the given polynomial.

Answer: None