Please help me I will really appreciate it!!!

Question

asked Jul 28, 2021 152k views

1 Answer

Applicative · Answer 1 · 2021-08-03T22:32:51+0000

Answer:

$\displaystyle r=\sqrt[3]{(3V)/(4\pi)}$

The last option matches the correct solution

Explanation:

Equation Solving

We have the following equation:

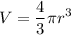
$\displaystyle V=(4)/(3)\pi r^3$

And it's required to solve it for r.

Solving this equation needs to perform some operations to have the r isolated from any other variables or constants.

It can be done by conveniently operating on both sides as follows:

Eliminate the denominator by multiplying by 3:

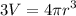
$\displaystyle 3V=4\pi r^3$

Move
$4\pi$ to the other side by dividing by
$4\pi$ :

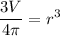
$\displaystyle (3V)/(4\pi)= r^3$

Swapping sides to have r at the left side:

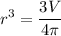
$\displaystyle r^3=(3V)/(4\pi)$

Finally, take the cubic root and leave r alone:

$\displaystyle r=\sqrt[3]{(3V)/(4\pi)}$

The last option matches the correct solution