Answer:
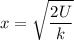
The third option is the correct answer.
Explanation:
Equation Solving
We have the following equation:
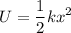
And it's required to solve it for x.
To solve this equation we need to perform some operations to have the x isolated from any other variables, constants, or operations.
This will be done by conveniently operating on both sides as follows:
Eliminate the denominator by multiplying by 2:

Move k to the other side by dividing by k:
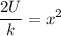
Swapping sides to have x at the left side:
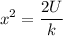
Taking the square root:
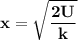
The third option is the correct answer.