Question

For the function below, (a) find the vertex; (b) find the axis of symmetry; (c) determine whether there is a maximum or a

minimum value and find that value; and (d) graph the function.
f(x) = -x2 - 6x-4

Answer 1

Explanation:

f(x) = ax² + bx + c

"x" coordinate of vertex is ( -
`(b)/(2a)` )

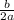axis of symmetry is x = -
`(b)/(2a)`

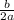
If a > 0 the function opens upward and has minimum value.

If a < 0 the function opens downward and has maximum value.

f(x) = - x² - 6x - 4

(a). x = -
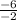`(-6)/(-2)` = - 3 ; y = - (- 3)² - 6( - 3) - 4 = 5

Coordinates of vertex are (- 3, 5)

(b). The axis of symmetry is x = - 3

(c). The given function opens downward

y = 5 is a maximum of a given function.