Answer:
3:36PM
Step-by-step explanation:
Leon starts at 12PM with 12 gallons of gas, and after 2 hours he has used 5 gallons of gas. This means that every 2 hours he uses 5 gallons of gas.
Next we will find at what point Leon will stop to get gas. Since he will stop when the tank is at
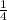 capacity, we can use the equation:
capacity, we can use the equation:
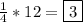
This shows
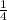 of his tank's capacity (
of his tank's capacity (
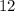 ) is equal to
) is equal to
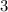 gallons. This means he will stop for gas when
gallons. This means he will stop for gas when
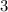 gallons are remaining.
gallons are remaining.
Now we need to find how many gallons of gas he uses, but as a unit rate. (This will allow us to find what time Leon will stop to get gas.) To find the unit rate, we will need to find how many gallons of gas he uses per hour.
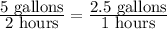
This is a simple proportion, and now we know he uses
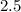 gallons of gas per hour.
gallons of gas per hour.
Now we can how many hours of gas Leon has left.
He has
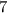 gallons of gas left at 2PM, so we can divide to find how many hours left of gas he has.
gallons of gas left at 2PM, so we can divide to find how many hours left of gas he has.
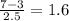
The
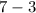 is because Leon doesn't stop when his tank is empty, he stops
is because Leon doesn't stop when his tank is empty, he stops
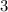 gallons earlier. We are dividing by
gallons earlier. We are dividing by
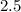 because that is how much gas he uses per hour, meaning the result of this division (
because that is how much gas he uses per hour, meaning the result of this division (
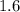 ) is how many hours he has left.
) is how many hours he has left.
Now we can solve for what time Leon will stop to get gas.
12PM +
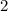 hours of driving + the remaining
hours of driving + the remaining
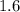 hours = 3:36PM
hours = 3:36PM
(
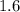 hours is equal to 1 hour and 36 minutes)
hours is equal to 1 hour and 36 minutes)
Therefore, Leon will stop for gas at 3:36PM