Question

Find the area of a triangle whose vertices are located at (-2,5), (-4, -3), and (3,1). Evaluate the determinant using diagonals.

Answer 1

The area of the triangle is 48 unit²

Explanation:

The given vertices of the triangle are;

(-2, 5), (-4, -3), and (3, 1)

The formula for finding the area of a triangle with given coordinates of the vertices is as follows;

`\Delta = (1)/(2)* \begin{vmatrix}x_1 & y_1 & 1\\ x_2 & y_2 & 1\\ x_3 & y_3 & 1\end{vmatrix} = (1)/(2)* \left | x_1\cdot y_2 - x_2\cdot y_1 + x_2\cdot y_3 - x_3\cdot y_2 + x_3\cdot y_1 - x_1\cdot y_3\right |`

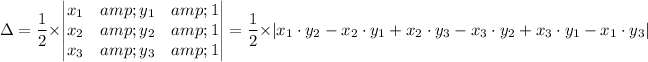
Substituting gives;

`\Delta = (1)/(2)* \begin{vmatrix}-2& 5 & 1\\ -4 & -3 & 1\\ 3 & 1 & 1\end{vmatrix} \\\Delta = (1)/(2)* \left | (-2)* (-3) - ((-4)* 5) + (-4)* 1 - 3* (-3) + 3 * 5 - (-2)* 1\right | \\\Delta = (1)/(2)* \left | 6 +20 -4 +9 + 15+2\right | = 48`

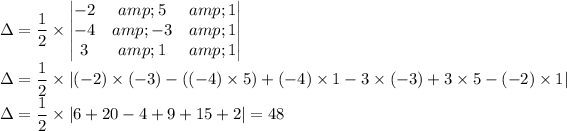
The area of the triangle = 48 unit².