Question

If f(x) = 16x – 30 and g(x) = 14x – 6, for which value of x does (f – g)(x) = 0? –18 –12 12 18

Answer 1

Option 3: 12 is the correct answer.

Explanation:

Given functions are:

`f(x) = 16x-30\\g(x) = 14x-6`

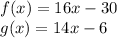
In order to find the value of x on which (f-g)(x) will be zero, first of all we have to find (f-g)(x) and then equate it equal to zero to find the value of that will make (f-g)(x)

So,

`(f-g)(x) = f(x) - g(x)\\= (16x-30)-(14x-6)\\=16x-30-14x+6\\= 2x-24`

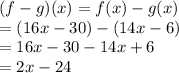
Now to find the value of x on which (f-g)(x) will be zero, putting (f-g)(x) = 0

`(f-g)(x) = 0\\2x-24 = 0`

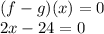
Adding 24 on both sides

`2x-24+24 = 0+24\\2x = 24`

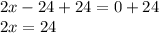
Dividing both sides by 2

`(2x)/(2) = (24)/(2)\\x = 12`

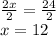
For x=12, (f-g)(x) will be zero.

Hence,

Option 3: 12 is the correct answer.