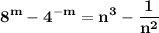Question

`{2}^(m) = n`
solve

`{8}^(m) - {4}^( - m)`
​

Answer 1

`\displaystyle n^3-(1)/(n^(2))`

Explanation:

Exponents Properties

We need to recall the following properties of exponents:

`(a^x)^y=(a^y)^x=a^(xy)`

`\displaystyle a^(-x)=(1)/(a^x)`

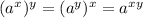
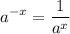
We are given the expression:

`2^m=n`

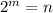
We need to express the following expression in terms of n.

`8^m-4^(-m)`

It's necessary to modify the expression to use the given equivalence.

Recall
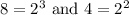`8=2^3 \text{ and }4 = 2^2`. Thus:

`(2^3)^m-(2^2)^(-m)`

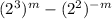
Applying the property:

`(2^m)^3-(2^m)^(-2)`

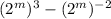
Substituting the given expression:

`n^3-n^(-2)`

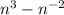
Or, equivalently:

`\mathbf{\displaystyle 8^m-4^(-m)= n^3-(1)/(n^(2))}`