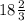Question

The sum of two number is 18. 5 times the first number subtracted from 4/7bof the second number is 14. Find the number

Answer 1

The numbers are
`-(2)/(3)` and
`18(2)/(3)`

Explanation:

Let x and y be the numbers

According to the statement, "The sum of two number is 18.", first equation will be:

`x+y = 18\ \ \ \ Eqn\ 1`

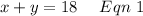
And according to "The sum of two number is 18. 5 times the first number subtracted from 4/7bof the second number is 14." Second equation will be:

`(4)/(7)y-5x = 14`

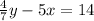
Multiplying whole equation by 7

`7*(4)/(7)y-7*5x = 7*14\\4y-35x=98\\-35x+4y = 98\ \ \ \ Eqn\ 2`

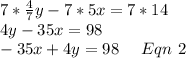
From equation 1

`x+y = 18\\y = 18-x`

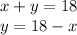
Putting this in second equation

`-35x+4(18-x) = 98\\-35x+72-4x= 98\\-39x = 98-72\\-39x = 26\\(-39x)/(-39) = (26)/(-39)\\x = -(2)/(3)`

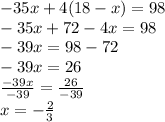
Putting x = -2/3 in equation 1

`-(2)/(3)+y = 18\\y = 18+(2)/(3)\\y = 18(2)/(3)`

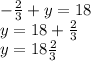
Hence, the numbers are
`-(2)/(3)` and
`18(2)/(3)`