Question

Answer this question in 20 mins timer start now or else the question will go away and u would give point 25 points Ready Set GOOOO!!

Answer 1

cost of a doughnut is $0.75

cost of a cookie is $0.60

Explanation:

As you wrote:
Let x = doughnuts

Let y = cookies

The first sentence of the problem (alexandra) can be written as:

`2x + 3y = 3.30`

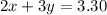
The second sentence of the equation (briana) can be written as:

`5x + 2y = 4.95`

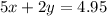
We must now solve for either
`x` or
`y` in this system of equations.

I will solve for
`x` in this example.

First we need to multiply the first equation by
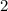`2` and the second equation by
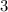`3`. This is so both equations have
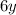`6y` as a term.

Equation 1:

`2(2x + 3y) = (3.30)2\\4x + 6y = 6.60`

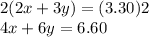
Equation 2:

`3(5x + 2y) = (4.95)3\\15x+6y=14.85`

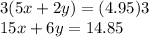
Now that both equations have
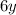`6y` as a term, we can subtract Equation 1 from Equation 2. This will remove y from the equation and allow us to solve for x.

`(15x+6y) - (4x+6y) = (14.85) - (6.60)\\11x = 8.25\\\boxed{x = 0.75}`

We now know the cost of a doughnut is $0.75. Now we can solve for the cost of a cookie through substitution.

`2x + 3y = 3.30\\2(0.75) + 3y = 3.30\\1.50 + 3y = 3.30\\3y = 1.80\\\boxed{y = 0.6}`

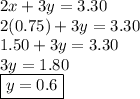
Now we know the cost of a cookie is $0.60.

These are the answers,

- Kan Academy Advance