Question

Question: Using only reciprocal, Pythagorean, sum/difference, and/or half angle identities, prove the equation below. You must use angles A and B, do not replace with actual vales. Only work with the right side of the equation. You should use TEN steps to accomplish this proof! cosA+cosB= 2cos(A+B/2)cos(A-B/2)​

Answer 1

See explanation below

Explanation:

Recall the identity for the cosine of an addition of angles:

`cos(\theta+\gamma)= cos(\theta)*cos(\gamma)- sin(\theta)*sin(\gamma)`

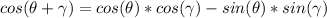
and that for a subtraction of angles:

`cos(\theta-\gamma)= cos(\theta)*cos(\gamma)+sin(\theta)*sin(\gamma)`

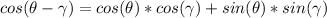
Now, use the property of addition of angles above to write :

`cos((A+B)/(2) +(A-B)/(2) )=cos((A+B)/(2) )*cos((A-B)/(2) )-sin((A+B)/(2) )*sin((A-B)/(2) )`

but since :
`(A+B)/(2) +(A-B)/(2)= A`

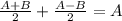
Then the cosine of addition of angles above can be written as:

`cos((A+B)/(2) +(A-B)/(2) )=cos((A+B)/(2) )*cos((A-B)/(2) )-sin((A+B)/(2) )*sin((A-B)/(2) )\\cos(A)=cos((A+B)/(2) )*cos((A-B)/(2) )-sin((A+B)/(2) )*sin((A-B)/(2) )`

We do something similar now with the cosine of the subtraction of angles:

`cos((A+B)/(2) -(A-B)/(2) )=cos((A+B)/(2) )*cos((A-B)/(2) )+sin((A+B)/(2) )*sin((A-B)/(2) )`

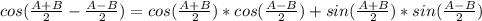
and we notice that:
`(A+B)/(2) -(A-B)/(2)= B`

Then the cosine of subtraction of angles above can be written as:

`cos((A+B)/(2) -(A-B)/(2) )=cos((A+B)/(2) )*cos((A-B)/(2) )+sin((A+B)/(2) )*sin((A-B)/(2) )\\cos(B )=cos((A+B)/(2) )*cos((A-B)/(2) )+sin((A+B)/(2) )*sin((A-B)/(2) )`

and finally, we add term by term the expressions we got for cos (A) and for cos(B) and notice that the terms that contain the sine functions cancel each other because they have opposite signs, while the terms in cosine add up to double themselves:

`cos(A )=cos((A+B)/(2) )*cos((A-B)/(2) )+sin((A+B)/(2) )*sin((A-B)/(2) )\\+\\cos(B )=cos((A+B)/(2) )*cos((A-B)/(2) )-sin((A+B)/(2) )*sin((A-B)/(2) )\\=\\cos(A) +cos(B)=2\,cos((A+B)/(2) )*cos((A-B)/(2) )`

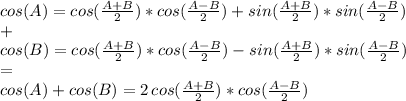
which is what we wanted to prove.