Question

A political candidate has asked his/her assistant to conduct a poll to determine the percentage of people in the community that supports him/her. If the candidate wants a 10% margin of error at a 90% confidence level, what size of sample is needed? Be sure to round accordingly. The candidate would need to survey people in the community in order to be within a 10% margin of error at a 90% confidence level.

Answer 1

The size of the sample needed = 67.65

Step-by-step explanation:

Given that :

The margin of error = 10% = 0.10

The confidence level = 90% = 0.90

Level of significance = 1 - 0.90 = 0.10

At ∝ = 0.10

`Z_(\alpha/2)= Z_(0.10/2) = 1.645`

Since the proportion of people that supported him/her is not given, we assumed p = 0.50

The margin of error formula can be expressed as:

`M.O.E = Z_(\alpha/2) * \sqrt{(p(1-p))/(n)}`

`0.10 = 1.645 * \sqrt{{(0.5(1-0.5))/(n)`

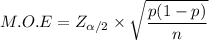
Squaring both sides; we have:

`0.10^2 = 1.645^2 * {(0.5(1-0.5))/(n)`

`0.01 = 2.706025 * (0.25)/(n)`

`n= 2.706025 * (0.25)/(0.01 )`

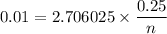
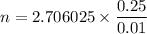
n = 67.65

Therefore, the required sample size = 67.65