Question

Test the claim that the mean GPA of night students is larger than 2 at the .025 significance level. The null and alternative hypothesis would be: H 0 : μ = 2 H 0 : μ = 2 H 1 : μ > 2 H 1 : μ > 2 H 0 : p = 0.5 H 0 : p = 0.5 H 1 : p ≠ 0.5 H 1 : p ≠ 0.5 H 0 : p = 0.5 H 0 : p = 0.5 H 1 : p > 0.5 H 1 : p > 0.5 H 0 : μ = 2 H 0 : μ = 2 H 1 : μ < 2 H 1 : μ < 2 H 0 : p = 0.5 H 0 : p = 0.5 H 1 : p < 0.5 H 1 : p < 0.5 H 0 : μ = 2 H 0 : μ = 2 H 1 : μ ≠ 2 H 1 : μ ≠ 2 Based on a sample of 60 people, the sample mean GPA was 2.02 with a standard deviation of 0.06 The test statistic is (to 3 decimals) The critical value is (to 3 decimals) Based on this we fail to reject the null hypothesis reject the null hypothesis

Answer 1

`H_0: \, \mu = 2`.

`H_1:\, \mu > 2`.

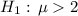Test statistics:
`z \approx 2.582`.

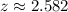Critical value:
`z_(1 - 0.025) \approx 1.960`.

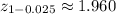Conclusion: reject the null hypothesis.

Explanation:

The claim is that the mean
`\mu` is greater than
`2`. This claim should be reflected in the alternative hypothesis:

`H_1:\, \mu > 2`.

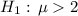The corresponding null hypothesis would be:

`H_0:\, \mu = 2`.

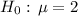In this setup, the null hypothesis
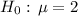`H_0:\, \mu = 2` suggests that
`\mu_0 = 2` should be the true population mean of GPA.

However, the alternative hypothesis
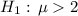`H_1:\, \mu > 2` does not agree; this hypothesis suggests that the real population mean should be greater than
`\mu_0= 2`.

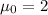One way to test this pair of hypotheses is to sample the population. Assume that the population mean is indeed
`\mu_0 = 2` (i.e., the null hypothesis is true.) How likely would the sample (sample mean
`\overline{X} = 2.02` with sample standard deviation
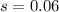`s = 0.06`) be observed in this hypothetical population?

Let
`\sigma` denote the population standard deviation.

Given the large sample size
`n = 60`, the population standard deviation should be approximately equal to that of the sample:

`\sigma \approx s = 0.06`.

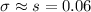Also because of the large sample size, the central limit theorem implies that
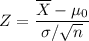`Z= \displaystyle \frac{\overline{X} - \mu_0}{\sigma / √(n)}` should be close to a standard normal random variable. Use a
`Z`-test.

Given the observation of
`\overline{X} = 2.02` with sample standard deviation
`s = 0.06`:

`\begin{aligned}z_\text{observed}&= \frac{\overline{X} - \mu_0}{\sigma / √(n)} \\ &\approx \frac{\overline{X} - \mu_0}{s / √(n)} = (2.02 - 2)/(0.06 / √(60)) \approx 2.582\end{aligned}`.

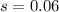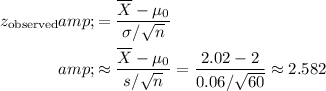Because the alternative hypothesis suggests that the population mean is greater than
`\mu_0 = 2`, the null hypothesis should be rejected only if the sample mean is too big- not too small. Apply a one-sided right-tailed
`z`-test. The question requested a significant level of
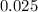`0.025`. Therefore, the critical value
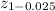`z_(1 - 0.025)` should ensure that
`P( Z > z_(1 - 0.025)) = 0.025`.

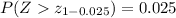Look up an inverse
`Z` table. The
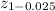`z_(1 - 0.025)` that meets this requirement is
`z_(1 - 0.025) \approx 1.960`.

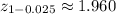The
`z`-value observed from the sample is
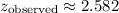`z_\text{observed}\approx 2.582`, which is greater than the critical value. In other words, the deviation of the sample from the mean in the null hypothesis is sufficient large, such that the null hypothesis needs to be rejected at this
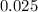`0.025` confidence level in favor of the alternative hypothesis.