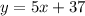Question

Consider the line y=5x -3 Find the equation of the line that is patellar to this line and passes through the point (-8, -3) Consider the line y=5x -3

Answer 1

The equation of the line that is parallel to given line and passes through the point (-8, -3) is:
`y = 5x+37`

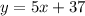
Explanation:

Given equation of line is:

`y=5x-3`

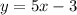
The general form of equation of line in slope-intercept form is written as:

`y = mx+b`

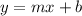
Here m(co-efficient of x) is the slope of the line and b is the y-intercept.

Comparing the given equation with the general form we get

m = 5

Two parallel lines have same slope so the slope of any line parallel to given line will also be 5.

Let m1 be the slope of required line parallel to y=5x-3

Then m1=5

Putting in general form

`y = m_1x+b`

`y=5x+b`

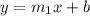
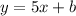
To find the value of b(y-intercept) the given point has to be put in the equation from which the line passes.

The point is (-8,-3)

`-3 = 5(-8)+b\\-3 = -40+b\\b = -3+40\\b = 37`

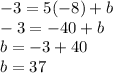
Putting the value of b and m1, we get

`y = 5x+37`

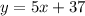
Hence,

The equation of the line that is parallel to given line and passes through the point (-8, -3) is:
`y = 5x+37`