Question

A balloon is launched straight upward and has a hang time of 14 s. (wow)

A.) What was the launching velocity of the balloon?
B.) How high did the balloon travel?
C.) How far did the balloon travel between t = 3 and t = 4 s?

Answer 1

A) Vo = 137.34 [m/s]

B) Y = 961.38 [m]

C) y = 367.8[m] for t = 3 [s] and y = 470.88[m] for t = 4[s]

Step-by-step explanation:

To solve this problem we must use the following equation of kinematics. We must keep in mind that the negative sign of the equation means that the acceleration of gravity acts in the opposite direction to the movement of the balloon.

A)

`v_(f) =v_(o) -g*t`

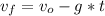
where:

Vf = final velocity = 0 (the maximum hang time, maximum elevation)

Vo = initial velocity [m/s]

g = gravity acceleration = 9.81 [m/s²]

t = time = 14 [s]

0 = Vo - (9,81*14)

Vo = 137.34 [m/s]

B)

Now we use the following equation.

`y=y_(o)+v_(o) *t -((1)/(2) )*g*t^(2)`

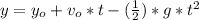
where:

Yo = initial position = 0

Y = final position [m]

Vo = initial velocity = 137.34 [m/s]

Now replacing

Y = (137.34*14) - (0.5*9.81*14²)

Y = 961.38 [m]

C)

With the above equation, we can calculate the distances between t = 3 and t = 4 [s]

`y=y_(o) +v_(o) *t - (1/2)*g*t^(2)`

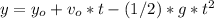
y = (137.34*3) - (0.5*9.81*3²)

y = 367.8[m] for t = 3 [s]

for t = 4[s]

y = (137.34*4) - (0.5*9.81*4²)

y = 470.88[m]