Answer:
d(P,Q) = 5.83 units
Mid-point = (23.5,25.5)
Explanation:
Given points are:
P(21,24) = (x1,y1)
Q(26,27) = (x2,y2)
The distance formula is given by:
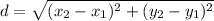
Here (x1,y1) are the coordinates of first point and (x2,y2) are coordinates of second point.
Putting the given values in the formula
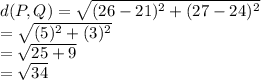
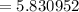
Rounding off: 5.83 units
The mid-point of two points is given by the formula:
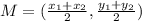
Putting the values:
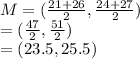
Hence,
d(P,Q) = 5.83 units
Mid-point = (23.5,25.5)