Question

Find the value of x in each case:

Answer 1

The value of x is 17

Explanation:

From the given figure

∵ AD ∩ BE at point C

∴ ∠ACB and ∠DCE are vertically opposite angles

∵ The vertically opposite angles are equal in measures

∴ m∠ACB = m∠DCE

→ The sum of interior angles of any Δ is 180°

∴ m∠A + m∠B + m∠ACB = 180°

∴ m∠D + m∠E + m∠DCE = 180°

→ Since the right sides equal, then equate the left sides

∵ m∠A + m∠B + m∠ACB = m∠D + m∠E + m∠DCE

→ Cancel the two equal angles ACB and DCE

∴ m∠A + m∠B = m∠D + m∠E

∵ m∠A = 4x, m∠B = 49°

∵ m∠D = 100°, m∠E = x

→ Substitute them in the equation above

∴ 4x + 49 = 100 + x

→ Subtract x from both sides

∵ 4x - x + 49 = 100 + x - x

∴ 3x + 49 = 100

→ Subtract 49 from both sides

∴ 3x + 49 - 49 = 100 - 49

∴ 3x = 51

→ Divide both them by 3 to find x

∵
`(3x)/(3)` =
`(51)/(3)`

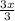∴ x = 17

∴ The value of x is 17