Question

5) A rectangular box 25cm by 20cm by 15cm internally is made of wood

0.5cm thick. If the box has a lid, find the volume of the wood used in cm'.

Answer 1

The volume of the wood used is
`1,116\ cm^3`

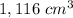
Explanation:

The Volume of a Rectangular Cuboid

In a rectangular cuboid, all angles are right, and the opposite faces are equal.

The volume of a cuboid of dimensions a,b,c is:

V=a.b.c

The rectangular box is made of wood with externals dimensions of 25 cm by 20 cm by 15 cm.

The external volume of the box is:

`V_e=(25)*(20)*(15)=7,500\ cm^3`

The walls of the box are 0.5 thick each, this means that the internal dimensions are 1 cm less than the external dimensions, including the lid.

Thus the internal volume is:

`V_i=(24)*(19)*(14)=6,384\ cm^3`

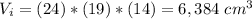
The volume of the wood used is the difference between the external and the internal volumes:

`V_w=7,500\ cm^3-6,384\ cm^3=1,116\ cm^3`

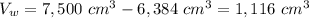
The volume of the wood used is
`\mathbf{1,116\ cm^3}`