Question

An integer is 15 more than 2 times another. If the product of the two integers is -27, then find the integers

Answer 1

The required integers are x=3 and y= -9

Explanation:

Let one the integers be x and y

An integer is 15 more than 2 times another: x=15+2y

product of the two integers is -27: x*y=27

`x=15+2y ---eq(1)\\x*y=-27----eq(2)`

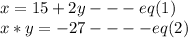
Solving both equations to find values of x and y

Putting value of x from equation 1 in equation 2

`(15+2y)*y=-27\\15y+2y^2=-27\\Rearranging:\\2y^2+15y-27=0`

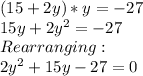
This can be solved using quadratic formula:

`$y=(-b\pm√(b^2-4ac))/(2a)$`

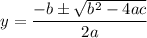
Putting values and finding factors

`$y=(-(15)\pm√((15)^2-4(2)(-27)))/(2(2))$\\$y=(-(15)\pm√(225+216))/(4)$\\$y=(-(15)\pm√(441))/(4)$\\$y=(-(15)\pm21)/(4)$\\$y=(-(15)+21)/(4) \ or \ y=(-(15)-21)/(4)$\\$y=(6)/(4) \ or \ y=(-36)/(4)$\\$y=(3)/(2) \ or \ y=-9$`

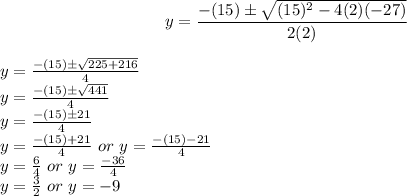
Since y is integer so, we consider only y= -9

The value of x will be:

`x*y=-27\\x*(-9)=-27\\x=(-27)/(-9) \\x=3`

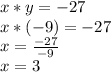
So, the value of x is x=3

The required integers are x=3 and y= -9