Answer:
The required integers are x=3 and y= -9
Explanation:
Let one the integers be x and y
An integer is 15 more than 2 times another: x=15+2y
product of the two integers is -27: x*y=27
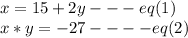
Solving both equations to find values of x and y
Putting value of x from equation 1 in equation 2
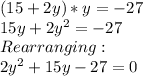
This can be solved using quadratic formula:
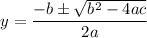
Putting values and finding factors
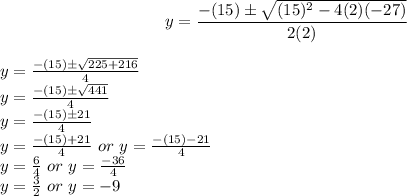
Since y is integer so, we consider only y= -9
The value of x will be:
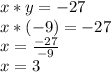
So, the value of x is x=3
The required integers are x=3 and y= -9