Answer:
1.7 m
Step-by-step explanation:
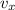 = Velocity of ball in x direction = 4.47 m/s
= Velocity of ball in x direction = 4.47 m/s
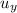 = Velocity of ball in y direction = 0
= Velocity of ball in y direction = 0
g = Acceleration due to gravity =
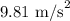
t = Time taken
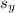 = Vertical displacement = 0.7 m
= Vertical displacement = 0.7 m
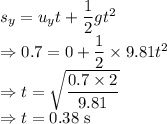
Horizontal displacement is given by
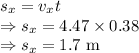
The passenger should throw the ball 1.7 m in front of the bucket.