Given:
In △ABC is a right angle triangle.
AC is 6 units longer than side BC.
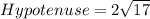
To find:
The length of AC.
Solution:
Let the length of BC be x.
So, Length of AC = x+6
According to the Pythagoras theorem, in a right angle triangle
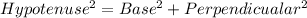
△ABC is a right angle triangle and AC is hypotenuse, so
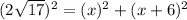
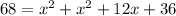
![[\because (a+b)^2=a^2+2ab+b^2]](https://img.qammunity.org/2021/formulas/mathematics/high-school/6n8c3v9pbdoizwtvjrtozuykapi2tgdl8o.png)
Subtract 68 from both sides.
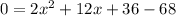
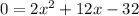
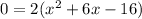
Divide both sides by 2.
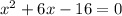
Splitting the middle term, we get
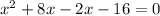
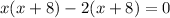
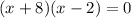
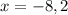
Side cannot be negative, so x=2 only.
Now,
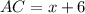
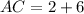
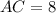
Therefore, the length of AC is 8 units.