Question

Determine the measure of angle a. PLEASE HELP ASAP!

a.64 degrees
b.45 degrees
c.88 degrees
d.42 degrees

Answer 1

D

Explanation:

Remember that the sum of the interior angles of a triangle will always total 180.

Therefore:

`(9x+6)+(74)+(16x)=180\\`

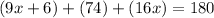
Let’s solve for x:

Combine LIke Terms:

`(9x+16x)+(74+6)=180`

Add:

`25x+80=180`

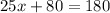
Subtract 80 from both sides:

`25x=100`

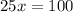
Divide both sides by 25:

`x=4`

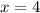
Therefore, the value of x is 4.

Now, to find A, we can substitute it for A.

A is measured by:

`\angle A=9x+6`

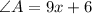
Substitute 4 for x and evaluate:

`\angle A=9(4)+6=36+6=42\textdegree`

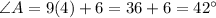
Hence, our answer is D.