Question

Peter works as a delivery person for a bike shipping company. The graph shows a linear model for his delivery times on different days. Peter’s Deliveries What is the equation of the line, first written in point-slope form, and then written in slope-intercept form? Show how you determined the equation. Based on the linear model, predict how long it initially took Peter to deliver his packages (y-intercept). Approximately how much did his delivery time decrease per day (slope)? Complete sentences.I need this done before Monday, please!

Answer 1

Answer/Step-by-step explanation:

✍️The equation of the line in point-slope form:

The equation is given as
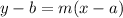`y - b = m(x - a)`, where,

(a, b) = a point on the line.

`slope (m) = (y_2 - y_1)/(x_2 - x_1)`

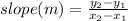
Let's find the slope (m) of the line, housing (3, 21) and (6, 12):

`slope (m) = (y_2 - y_1)/(x_2 - x_1) = (12 - 21)/(6 - 3) = (-9)/(3) = -3`

Substitute a = 3 and b = 21, m = -3 into
`y - b = m(x - a)`.

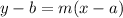Thus, the point-slope equation would be:

✅
`y - 21 = -3(x - 3)`

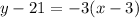
✍️The equation of the line in slope-intercept form:

Rewrite
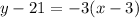`y - 21 = -3(x - 3)`, so that y is made the subject of the formula.

`y - 21 = -3x + 9`

Add 21 to both sides

`y = -3x + 9 + 21`

`y = -3x + 30`

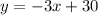
✅The slope-intercept equation of the line is
`y = -3x + 30`

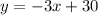
Where,

-3 = how much did his delivery time decrease per day (slope)

30 = how long it initially took Peter to deliver his packages (y-intercept)