Answer:
Magnitude of gravitational force between this planet and its moon: approximately
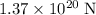 .
.
Acceleration of this moon towards the planet: approximately
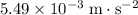 .
.
Acceleration of this planet towards its moon: approximately
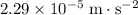 .
.
Step-by-step explanation:
Look up the gravitational constant,
 :
:
 .
.
Assume that both this planet and its moon are spheres of uniform density. When studying the gravitational interaction between this planet and its moon, this assumption allows them to be considered as two point masses.
The formula for the size of gravitational force between two point masses
 and
and
 with a distance of
with a distance of
 in between is:
in between is:
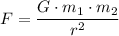 ,
,
where
 is the gravitational constant.
is the gravitational constant.
Let
 and
and
 denote the mass of this planet and its moon, respectively.
denote the mass of this planet and its moon, respectively.
Calculate the size of gravitational force between this planet and its moon:
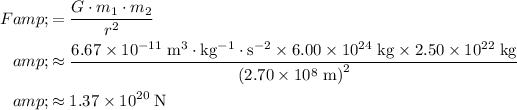 .
.
Assume that other than the gravitational force between this planet and its moon, all other forces (e.g., gravitational force between this planet and the star) are negligible. The magnitude of the net force on the planet and on the moon should both be approximately
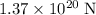 .
.
Apply Newton's Second Law of motion to find the acceleration of this planet and its moon:
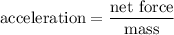 .
.
For this moon:
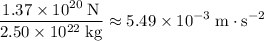 .
.
For this planet:
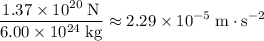 .
.