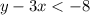Question

Which ordered pairs are solutions to the inequality y - 3x < -8?

Select each correct answer.
(1, -5)
(-3, - 2)
(0, -9)
(2, -1)
(5, 4)​​​

Answer 1

Option B,C and E are solution to given inequality
`y - 3x < -8`

Explanation:

We need to check which ordered pairs from given options satisfy the inequality
`y - 3x < -8`

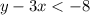
Ordered pairs are solutions to inequality if they satisfy the inequality

Checking each options by pitting values of x and y in given inequality

A ) (1, -5)

`-5-3(1)<-8\\-5-3<-8\\-8 < -8 \ (incorrect)`

So, this ordered pair is not the solution of inequality as it doesn't satisfy the inequality.

B) (-3, - 2)

`-2-3(-3) < -8\\-2-9<-8\\-11 < -8 (true)`

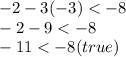
So, this ordered pair is solution of inequality as it satisfies the inequality.

C) (0, -9)

`-9-3(0)<-8\\-9-0<-8\\-9<-8 \ (true)`

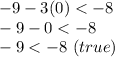
So, this ordered pair is solution of inequality as it satisfies the inequality.

D) (2, -1)

`-1-3(2)<-8\\-1-6<-8\\-7<-8 \ (false)`

So, this ordered pair is not the solution of inequality as it doesn't satisfy the inequality.

E) (5, 4)​​​

`4-3(5)<-8\\4-15<-8\\-11<-8 \ (true)`

So, this ordered pair is solution of inequality as it satisfies the inequality.

So, Option B,C and E are solution to given inequality
`y - 3x < -8`