Question

Find derivative for 3x³ + 2xy + 4y²=0.

Answer 1

`(dy)/(dx)= -(9x^2+2y)/(2(x+4y))`

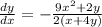
Explanation:

Find the derivative of
`3x^3 + 2xy + 4y^2 = 0`.

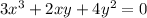In order to find the derivative of this function,
`(dy)/(dx)`, we can start by noticing that there are two variables in this problem, x and y.

Since we want the derivative with respect to x, every time we encounter the variable “y” in this problem we can change it to
`(dy)/(dx)`. We will see this happen later on in the solving process by using implicit differentiation.

Let’s start by taking the derivative of the entire function:

• 
  `(d)/(dx) (3x^3 + 2xy + 4y^2 = 0)`

Using the Power Rule and the Product Rule, we can perform implicit differentiation on this equation. Let’s take the derivative of each separate piece in this function:

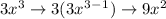`3x^3 \rightarrow 3(3x^3^-^1) \rightarrow 9x^2` Power Rule

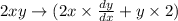`2xy \rightarrow (2x * (dy)/(dx) + y * 2)` Product Rule

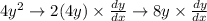`4y^2 \rightarrow 2(4y) * (dy)/(dx) \rightarrow 8y * (dy)/(dx)` Power Rule & Implicit Differentiation

Let’s combine these steps into one comprehensive operation:

• 
  `9x^2 + (2x * (dy)/(dx) + y * 2) + 8y * (dy)/(dx) = 0`

Simplify.

• 
  `9x^2 + 2x(dy)/(dx) + 2y + 8y (dy)/(dx) = 0`

Keep all terms containing
`(dy)/(dx)` on the left side of the equation and move everything else to the right side of the equation. This way we can solve for
`(dy)/(dx)`, which, in this case, is the derivative of the original function.

Subtract
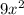`9x^2` and
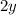`2y` from both sides of the equation.

• 
  `2x(dy)/(dx) +8y (dy)/(dx) = -9x^2-2y`

Factor out dy/dx from the left side of the equation.

• 
  `(dy)/(dx)(2x+8y) = -9x^2-2y`

Divide both sides of the equation by (2x + 8y).

• 
  `(dy)/(dx)= (-9x^2-2y)/(2x+8y)`

You can leave it in this form, or you can convert this to either:

• 
  `(dy)/(dx)= (-9x^2-2y)/(2(x+4y))`

• 
  `(dy)/(dx)= -(9x^2+2y)/(2(x+4y))`

Answer 2

`y'=(-9x^2-2y)/(2(x+4y))`

General Formulas and Concepts:

Algebra

• Equality Properties

Calculus

• Chain Rule:
  `(d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)`
• Basic Power Rule: f’(x) = c·nxⁿ⁻¹
• Derivative of a constant equals 0
• Implicit Differentiation

Explanation:

Step 1: Define equation

3x³ + 2xy + 4y² = 0

Step 2: Find 1st Derivative

1. Set up Derivative:
   `(dy)/(dx) [3x^3 + 2xy + 4y^2 = 0]`
2. Take Implicit Differentiation:
   `9x^2+(2y+2xy')+8yy'=0`

Step 3: Find Derivative (Solve for y')

1. Define:
   `9x^2+(2y+2xy')+8yy'=0`
2. Move 9x² over:
   `2y+2xy'+8yy'=-9x^2`
3. Move 2y over:
   `2xy'+8yy'=-9x^2-2y`
4. Factor y':
   `y'(2x+8y)=-9x^2-2y`
5. Isolate y':
   `y'=(-9x^2-2y)/(2x+8y)`
6. Factor GCF:
   `y'=(-9x^2-2y)/(2(x+4y))`