If the definitions of type I and type II regions is the same as in the link provided, then as a type I region the integration domain is the set

and as a type II region,
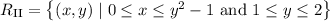
where we solve y = √(x + 1) for x to get x as a function of y.
A. The area of the type I region is
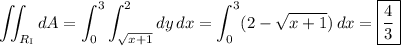
B. The area of the type II region is of course also
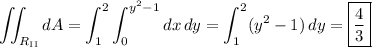
I've attached a plot of the type II region to give an idea of how it was determined. The black arrows indicate the domain of x as it varies from the line x = 0 (y-axis) to the curve y = √(x + 1).