Question

Hi! I just need somebody to explain how this is done.

I don’t understand the process of this well and I cant find many videos that explain it. thanks!

Answer 1

Exact form: x =
`(10.8)/(sin(57))`

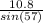
Rounded to the Nearest Tenth: x = 12.9

Explanation:

In the right-angled triangle, we can use the trigonometry functions to find the length of a side or a measure of an angle

In the given figure

∵ ∠C is the right angle

∴ ΔACB is a right triangle

∵ m∠B = 57°

∵ AC = 10.8

∵ AC is the opposite side of ∠B

∵ AB is opposite to the right angle

∴ AB is the hypotenuse

∵ AB = x

→ We can use the function sine to find x

∵ sin∠B =
`(opposite)/(hypotenuse)`

∴ sin∠B =
`(AC)/(AB)`

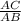
→ Substitute the values of ∠B, AC, and AB in the rule of sine above

∴ sin(57°) =
`(10.8)/(x)`

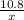
→ By using cross multiplication

∵ x × sin(57°) = 10.8

→ Divide both sides by sin(57°)

∴ x =
`(10.8)/(sin(57))`

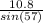
∴ x = 12.87752356

→ Round your answer to the nearest tenth

∴ x = 12.9

Exact form: x =
`(10.8)/(sin(57))`

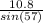
Rounded to the Nearest Tenth: x = 12.9