Question

The minimum/maximum value of the function y = a(x − 2)(x − 1) occurs at x = d, what is the value of d?

Answer 1

`d=(3)/(2)=1.5`

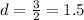
Explanation:

We have the function:

`y=a(x-2)(x-1)`

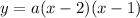
And we want to find x=d for which the minimum/maximum value will occur.

Notice that our function is a quadratic in factored form.

Remember that the minimum/maximum value always occurs at the vertex point.

And remember that the x-coordinate of the vertex is the axis of symmetry.

Since a quadratic is always symmetrical on both sides of its axis of symmetry, a quadratic’s axis of symmetry is the average of the two roots/zeros of the quadratic.

Therefore, the value x=d such that it produces the minimum/maximum value is the average of the two roots.

Our factors are (x-2) and (x-1).

Therefore, our roots/zeros are x=1, 2.

So, the average of them are:

`d=(1+2)/(2)=3/2=1.5`

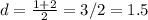
Therefore, regardless of the value of a, the minimum/maximum value will occur at x=d=1.5.

Alternative Method:

Of course, we can also expand to confirm our answer. So:

`y=a(x^2-2x-x+2)\\y=a(x^2-3x+2)\\y=ax^2-3ax+2a`

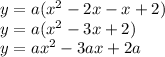
The x-coordinate of the vertex is still going to be the place where the minimum/maximum is going to occur.

And the formula for the vertex is:

`x=-(b)/(2a)`

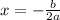
So, we will substitute -3a for b and a for a. This yields:

`x=-(-3a)/(2a)=(3)/(2)=1.5`

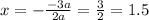
Confirming our answer.