Question

I need help on these problems THANK YOUUU

Answer 1

1 is (2.-2) but i cant see the rest

Explanation:

Answer 2

2. m = 1

3. y - (-1) = 5 (x - 4)

4. y = 5x - 21

Explanation:

Work for #2

m (slope) =
`(y2 - y1)/(x2 - x1) \fracyx}`

m =
`(-1 - 2)/(-2 -1)`

m =
`(-3)/(-3)`

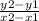
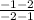
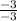
m = 1

Work for #3

y = -1/5x + 3 and through (4, -1)

The slope of a perperndicular line is the negative reciprocal. So, it is 5.

Plug this number into point-slope form. Use the points you were given (4,-1) in the equation as well.

y - y1 = m (x - x1)

y - (-1) = 5 (x - 4)

y + 1 = 5x - 20 (Only if you are supposed to simplify it)

Work for #4

Finish solving the equation

y - (-1) = 5 (x - 4)

y + 1 = 5x - 20

y = 5x - 20 - 1

y = 5x - 21