Question

Question 2

2.5 pts
A firefighter sees a woman trapped in a building 91 feet up from the bottom floor. If the
firetruck is parked 67 feet away from the bottom of the building, at what angle of elevation, to
the nearest degree, should the firefighter extend the ladder to reach the woman?
Previous

Answer 1

The firefighter should extend the ladder at 54° of elevation.

Explanation:

Trigonometric Ratios

The ratios of the sides of a right triangle are called trigonometric ratios. There are six trigonometric ratios, sine, cosine, tangent, cosecant, secant, and cotangent.

The longest side of the triangle is called the hypotenuse and the other two sides are the legs.

Selecting any of the acute angles as a reference, it has an adjacent side and an opposite side. The trigonometric ratios are defined upon those sides.

Tangent Ratio:

`\displaystyle \tan\theta=\frac{\text{opposite leg}}{\text{adjacent leg}}`

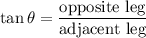
The woman is trapped at 91 feet up from the ground, and the firetruck is 67 feet away from the building.

The wall, the ground, and the ladder form a right triangle, where θ is the horizontal angle of the ladder.

Being the height of the woman the opposite leg and the distance where the firetruck is parked, the adjacent leg:

`\displaystyle \tan\theta=(91)/(67)=1.3582`

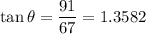
The angle is calculated as the inverse tangent:

`\theta=arctan(1.3582)\approx 54^\circ`

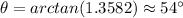
The firefighter should extend the ladder at 54° of elevation.