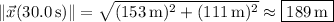We have the relation
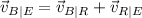
where
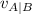 denotes the velocity of a body A relative to another body B; here I use B for boat, E for Earth, and R for river.
denotes the velocity of a body A relative to another body B; here I use B for boat, E for Earth, and R for river.
We're given speeds
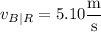
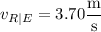
Let's assume the river flows South-to-North, so that
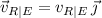
and let
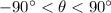 be the angle made by the boat relative to East (i.e. -90° corresponds to due South, 0° to due East, and +90° to due North), so that
be the angle made by the boat relative to East (i.e. -90° corresponds to due South, 0° to due East, and +90° to due North), so that
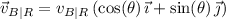
Then the velocity of the boat relative to the Earth is
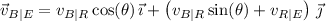
The crossing is 153.0 m wide, so that for some time
 we have
we have
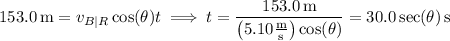
which is minimized when
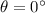 so the crossing takes the minimum 30.0 s when the boat is pointing due East.
so the crossing takes the minimum 30.0 s when the boat is pointing due East.
It follows that
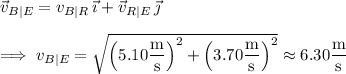
The boat's position
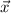 at time
at time
 is
is
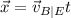
so that after 30.0 s, the boat's final position on the other side of the river is
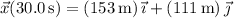
and the boat would have traveled a total distance of