Answer:
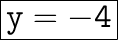
Explanation:
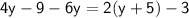
Subtract like terms : 6y from 4y
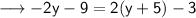
Distribute 2 through the parentheses
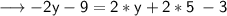
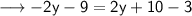
Subtract 3 from 10
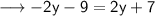
Move 2y to left hand side and change it's sign
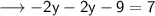
Move 9 to right hand side and change it's sign
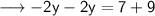
Combine like terms
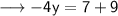
Add the numbers : 7 and 9
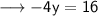
Divide both sides by -4
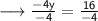
Remember : Dividing a positive integer by any negative integer gives a negative integer.
------------------------------------------------------------
Let's check whether the value of y is -4 or not.
Verification
L.H.S :
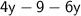
plug the value of y and simplify

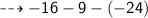
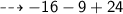
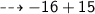
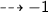
R.H.S :
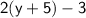
plug the value of y and simplify
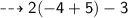

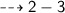
∴ L.H.S = R.H.S
The value of y is -4
And we're done!
------------------------------------------------------------
Rules for solving an equation
- If any equation contains fractions , multiply each term by the LCM of denominators.
- Remove the brackets , if any.
- Collect the terms with the variable to left hand side and constant terms to the right side by changing their signs ' + ' into ' - ' and ' - ' into ' + '.
- Simplify and get the single term on each side.
- Divide each side by the coefficient of variable and then get the value of variable.
Hope I helped!
Best regards! :D
~TheAnimeGirl