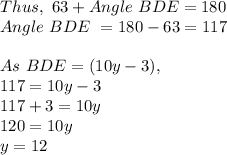Answer:
x=17, y=12
Explanation:
From the figure we know that,
Angle CDB = 4x-5
Angle BDE = 10y-3
Angle DEA= 97-2x
Though we are NOT given that line segments BD and AE are parallel, we may assume so by the construction of the triangle.
Hence, BD II AE and are cut by the transversal CE,
Hence,
Angle CDB = Angle CEA {Corresponding angles are equal}
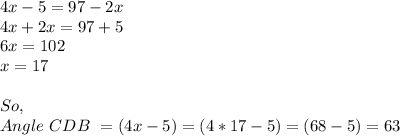
As we observe that,
Angle CDB and Angle BDE form a linear pair, they are supplementary.
Hence,
Angle CDB + Angle BDE = 180