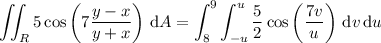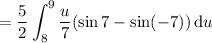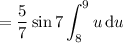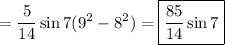Question

Evaluate the integral by making an appropriate change of variables.

Answer 1

By inspecting the integrand, the "obvious" choice for substitution would be

u = y + x

v = y - x

Solving for x and y, we would have

x = (u - v)/2

y = (u + v)/2

in which case the Jacobian and its determinant are

`J=\begin{bmatrix}x_u&x_v\\y_u&y_v\end{bmatrix}=\frac12\begin{bmatrix}1&-1\\1&1\end{bmatrix}\implies|\det J|=\left|\frac12\right|=\frac12`

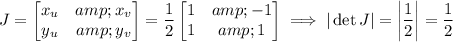
The trapezoid R has two of its edges on the lines x + y = 8 and x + y = 9, so right away, we have 8 ≤ u ≤ 9.

Then for v, we observe that when x = 0 (the lowest edge of R), v = y ; similarly, when y = 0 (the leftmost edge of R), v = -x. So

-x ≤ v ≤ y

-(u - v)/2 ≤ v ≤ (u + v)/2

-u + v ≤ 2v ≤ u + v

-u ≤ v ≤ u

So, the integral becomes

`\displaystyle\iint_R5\cos\left(7(y-x)/(y+x)\right)\,\mathrm dA=\int_8^9\int_(-u)^u\frac52\cos\left(\frac{7v}u\right)\,\mathrm dv\,\mathrm du`

`=\displaystyle\frac52\int_8^9\frac u7(\sin7-\sin(-7))\,\mathrm du`

`=\displaystyle\frac57\sin7\int_8^9u\,\mathrm du`

`=\displaystyle\frac5{14}\sin7(9^2-8^2)=\boxed{(85)/(14)\sin7}`