Question

Please help. Trigonometric ratios ​

Answer 1

Question 2.1.1

Answer: 5 units

Reason:

Use the distance formula to find the distance from the origin (0,0) to the terminal point (-3, 4)

`(x_1,y_1) = (0,0) \text{ and } (x_2, y_2) = (-3,4)\\\\d = √((x_1 - x_2)^2 + (y_1 - y_2)^2)\\\\d = √((0-(-3))^2 + (0-4)^2)\\\\d = √((0+3)^2 + (0-4)^2)\\\\d = √((3)^2 + (-4)^2)\\\\d = √(9 + 16)\\\\d = √(25)\\\\d = 5\\\\`

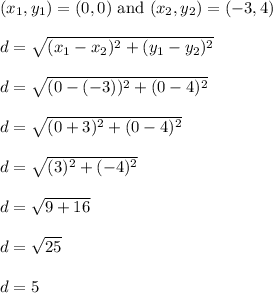
The pythagorean theorem is a similarly related alternative path you can take.

This triangle is a 3-4-5 right triangle.

====================================================

Question 2.1.2

Answer: 1/5

Reason:

r = distance from origin to terminal point

r = 5, calculated back in the previous problem above.

sin(alpha) = y/r = 4/5

cos(alpha) = x/r = -3/5

sin(alpha)+cos(alpha) = (4/5)+(-3/5) = 1/5

====================================================

Question 2.1.3

Answer: 1

Reason:

Recall that tangent is the ratio of sine over cosine

tan = sin/cos

Therefore,

`\tan(\alpha) *(\cos(\alpha))/(\sin(\alpha))\\\\(\sin(\alpha))/(\cos(\alpha))*(\cos(\alpha))/(\sin(\alpha))\\\\(\sin(\alpha)*\cos(\alpha))/(\cos(\alpha)*\sin(\alpha))\\\\1`

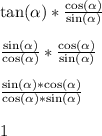
This assumes that neither sin(alpha) nor cos(alpha) are zero. Otherwise, we have a division by zero error.