Answer: No it is not a right triangle.
======================================================
Work Shown:
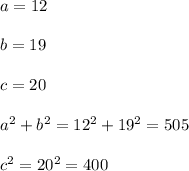
The values of
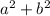 and
and
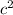 are not the same number
are not the same number
Therefore, there's no way that
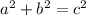 is possible, which means we do not have a right triangle.
is possible, which means we do not have a right triangle.
Put another way: since
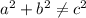 , this means we don't have a right triangle.
, this means we don't have a right triangle.
Refer to the converse of the pythagorean theorem for more information.
Side note: because of that same theorem, and because
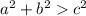 is the case, this means we have an acute triangle based on what is shown below.
is the case, this means we have an acute triangle based on what is shown below.