Question

A triangle has sides with lengths of 12 meters, 19 meters, and 20 meters. Is it a right triangle?

Answer 1

Answer: No it is not a right triangle.

======================================================

Work Shown:

`a = 12\\\\b = 19\\\\c = 20\\\\a^2+b^2 = 12^2+19^2 = 505\\\\c^2 = 20^2 = 400\\\\`

The values of
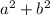`a^2+b^2` and
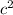`c^2` are not the same number

Therefore, there's no way that
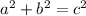`a^2+b^2 = c^2` is possible, which means we do not have a right triangle.

Put another way: since
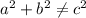`a^2+b^2 \\e c^2`, this means we don't have a right triangle.

Refer to the converse of the pythagorean theorem for more information.

Side note: because of that same theorem, and because
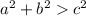`a^2+b^2 > c^2` is the case, this means we have an acute triangle based on what is shown below.