Answer:
The resultant of the given vectors by component method is
![\vec U = -8.222\,\hat{i}+35.664\,\hat{j}\,\,\,[km]](https://img.qammunity.org/2021/formulas/mathematics/college/uheb7tv6ktubu3lpr5mm6m5d4ezsbj5rv9.png) .
.
Explanation:
First we define each vector by applying using rectangular form:
1)
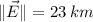 , 11º north of east.
, 11º north of east.
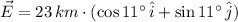 (Eq. 1)
(Eq. 1)
2)
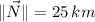 , 24º east of north.
, 24º east of north.
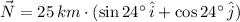 (Eq. 2)
(Eq. 2)
3)
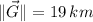 , 18º south of west.
, 18º south of west.
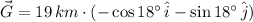 (Eq. 3)
(Eq. 3)
4)
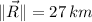 , 58º west of north.
, 58º west of north.
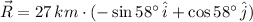 (Eq. 4)
(Eq. 4)
The resultant of given vectors is determined by vector sum, that is:
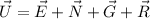 (Eq. 5)
(Eq. 5)
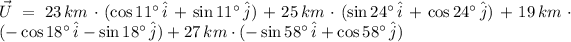
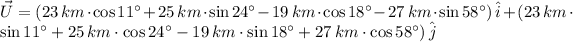
![\vec U = -8.222\,\hat{i}+35.664\,\hat{j}\,\,\,[km]](https://img.qammunity.org/2021/formulas/mathematics/college/uheb7tv6ktubu3lpr5mm6m5d4ezsbj5rv9.png)
The resultant of the given vectors by component method is
![\vec U = -8.222\,\hat{i}+35.664\,\hat{j}\,\,\,[km]](https://img.qammunity.org/2021/formulas/mathematics/college/uheb7tv6ktubu3lpr5mm6m5d4ezsbj5rv9.png) .
.