Answer:
The mass left after 24.6 years is 25.0563 grams
Step-by-step explanation:
The given parameters are;
The mass of the hydrogen-3 = 100 grams
The half life of hydrogen-3 which is also known as = 12.32 years
The formula for calculating half-life is given as follows;
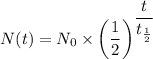
Where;
N(t) = The mass left after t years
N₀ = The initial mass of the hydrogen-3 = 100 g
t = Time duration of the decay = 24.6 years
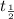 = Half-life = 12.32 years
= Half-life = 12.32 years
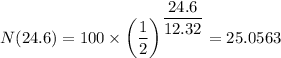
The mass left after 24.6 years = 25.0563 grams.