Answer:
The longest codeword that could possibly be for "n" symbol is n-1 bits.
Step-by-step explanation:
From the given information:
Suppose we are to consider a set of frequencies
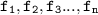 , for which f is a symbol for the length n. Therefore, the longest codeword that could possibly be for "n" symbol is n-1 bits.
, for which f is a symbol for the length n. Therefore, the longest codeword that could possibly be for "n" symbol is n-1 bits.
However, during the encoding for "n" in conjunction with n-2, then the possibilities for n are;
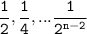
We can conclude that the longest codeword that could possibly be for "n" symbol is n-1 bits.