Question

An annealed copper strip of 228 mm wide and 25 mm thick being rolled to a thickness of 20 mm, in one pass. The roll radius is 300 mm, and the rolls rotate at 100 rpm. Calculate the roll force and the power required in this operation

Answer 1

The roll force is 1.59 MN

The power required in this operation is 644.96 kW

Step-by-step explanation:

Given;

width of the annealed copper, w = 228 m

thickness of the copper, h₀ = 25 mm

final thickness, hf = 20 mm

roll radius, R = 300 mm

The roll force is given by;

`F = LwY_(avg)`

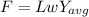
where;

w is the width of the annealed copper

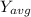`Y_(avg)` is average true stress of the strip in the roll gap

L is length of arc in contact, and for frictionless situation it is given as;

`L = √(R(h_o-h_f)) \\\\L = √(300(25-20))\\\\L = 38.73 \ mm`

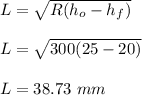
Now, determine the average true stress,
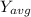`Y_(avg)`, for the annealed copper;

The absolute value of the true strain, ε = ln(25/20)

ε = 0.223

from true stress vs true strain graph; at true strain of 0.223, the true stress is 280 MPa.

Then, the average true stress = ¹/₂(280 MPa.) = 180 MPa

Finally determine the roll force;

`F = LwY_(avg)`

`F = ((38.73 )/(1000))((228)/(1000))*180 \ MPa\\\\F = 1.59 \ MN`

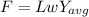
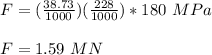
The power required in this operation is given by;

`P = (2\pi FLN)/(60)\\\\P = (2\pi (1.59*10^6)(0.03873)(100))/(60)\\\\P = 644955.2 \ W\\\\P = 644.96 \ kW`