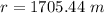Question

If the jet is moving at a speed of 1140 km/h at the lowest point of the loop, determine the minimum radius of the circle so that the centripetal acceleration at the lowest point does not exceed 6.0 g's.

Answer 1

The radius is
`r =1705.44 \ m`

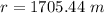
Step-by-step explanation:

From the question we are told that

The speed is
`v = 1140 \ km /h = (1140 * 1000)/(3600) = 316.67 \ m/s`

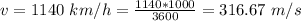
The centripetal acceleration is
`a = 6 g's = 6 * 9.8 = 58.8 \ m/s^2`

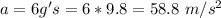
Generally the centripetal force acting on the jet is mathematically represented as

`F_c = (m * v^2 )/(r)`

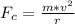
Generally this centripetal force is equal to the net force acting which according to Newton's third law is mathematically represented as

`F = m * a`

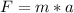
So

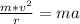
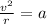
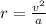
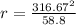
`(m * v^2 )/(r) = ma`

=>
`( v^2 )/(r) = a`

=>
`r = (v^2)/(a)`

=>
`r = (316.67^2)/(58.8)`

=>
`r =1705.44 \ m`