Question

If a second planet were of the same radius R and made of the same material but had a hollow center of radius 0.50 R , what would be the acceleration of gravity at its surface

Answer 1

`g_2=(7)/(8)g`

Step-by-step explanation:

G = Gravitational constant

M = Mass of planet

R = Radius of planet

Acceleration due to gravity on first planet

`g=(GM)/(R)`

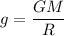
Assuming that the planets have the same mass density
`\rho`

Density of first planet

`\rho=(M)/(V)\\\Rightarrow \rho=(M)/((4)/(3)\pi R^3)\\\Rightarrow M=\rho (4)/(3)\pi R^3`

Density of second planet

`\rho=(M_2)/(V_2)=(M_2)/((4)/(3)\pi R^3-(4)/(3)\pi (0.5R)^3)\\\Rightarrow \rho=(M_2)/((4)/(3)\pi R^3(1-(1)/(2^3)))\\\Rightarrow \rho=(M_2)/((4)/(3)\pi R^3(1-(1)/(8)))\\\Rightarrow \rho=(M_2)/((4)/(3)\pi R^3((7)/(8)))\\\Rightarrow M_2=\rho(4)/(3)\pi R^3((7)/(8))\\\Rightarrow M_2=M(7)/(8)`

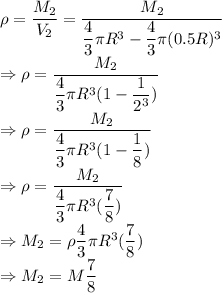
Acceleration due to gravity on the second planet

`g_2=(GM_2)/(R)\\\Rightarrow g_2=(GM(7)/(8))/(R)\\\Rightarrow g_2=(7)/(8)g`

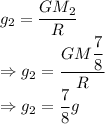
The acceleration due to gravity of the planet would be
`(7)/(8)` times the acceleration due to gravity on the first planet.