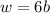Answer:
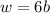
Explanation:
Given
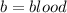
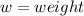
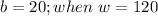
Required
Determine the equation that binds both parameters
First, we need to determine the constant of proportionality using:
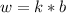
Where k represents the constant.
Substitute 120 for w and 20 for b
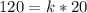
Divide both sides by 20
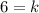
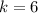
Using the same formula, substitute 6 for k
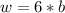
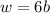
Hence:
The equation is represented as