Question

A 3.63.kgkg chihuahua charges at a speed of 3.3m/s3.3m/s. What is the magnitude of the average force needed to bring the chihuahua to a stop in 0.50s0.50s

Answer 1

The magnitude of the average force needed to bring the chihuahua to a stop is 23.96 N

Step-by-step explanation:

Newton's second law states that the acceleration of an object is inversely proportional to the mass of the object. The greater the mass of an object, the less its acceleration will be if a given net force is applied to it. In other words, mass is a property of objects that opposes acceleration when a force is applied.

In this way, Newton's second law says that the acceleration of a body is proportional to the resultant of forces on the acting and inversely proportional to its mass. This is expressed by the mathematical relationship:

F = m * a

where:

F = Force [N]

m = Mass [kg]

a = Acceleration [
`(m)/(s^(2) )`]

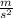You know that 3.63 kg chihuahua charges at a speed of 3.3m/s and you need to bring the chihuahua to a stop in 0.50s.

A motion is uniformly varied rectilinear when the trajectory of the mobile is a straight line and its speed varies by the same amount in each unit of time, so that the acceleration is constant. In this case the uniformly varied rectilinear motion is fulfilled. Being:

velocity (final) = velocity (initial) + acceleration * time

vf = vi + a * t

the acceleration is:

`a=(vf-vi)/(t)`

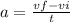
In this case:

• vf= 0
  `(m)/(s)` because the chihuahua stops.

• vi= 3.3
  `(m)/(s)`

• t=0.50 s

Replacing:

`a=(0(m)/(s) -3.3 (m)/(s) )/(0.50 s)`

Solving:

a= -6.6
`(m)/(s^(2) )`

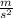
Then the magnitude of the average force can be calculated as:

F=m*a

F=3.63 kg* (-6.6
`(m)/(s^(2) )` )

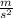Solving:

F= - 23.96 N

The magnitude of the average force needed to bring the chihuahua to a stop is 23.96 N

Answer 2

23.96 N

Step-by-step explanation:

From the question given above, the following data were obtained:

Mass of Chihuahua (m) = 3.63 kg

Velocity (v) = 3.3m/s

Time (t) = 0.50 s

Force (F) =?

Next, we shall determine the acceleration of the Chihuahua. This can be obtained as follow:

Velocity (v) = 3.3m/s

Time (t) = 0.50 s

Acceleration (a) =?

a = v/t

a = 3.3/0.5

a = 6.6 m/s²

Thus, the acceleration of the Chihuahua is 6.6 m/s².

Finally, we shall determine the force need to stop the Chihuahua as shown below:

Mass of Chihuahua (m) = 3.63 kg

Acceleration (a) = 6.6 m/s².

Force (F) =?

F = ma

F = 3.63 × 6.6

F = 23.96 N

Therefore, a force of 23.96 N is needed to stop the Chihuahua.